FACULTY
教員紹介
中川 智之 NAKAGAWA Tomoyuki
大学院
統計数理研究室
数学でデータを読み解く - 統計理論と実データ解析の融合
専門分野
- 数理統計学
- データ科学
研究テーマ
多変量統計解析
漸近統計解析
ベイズ統計
ロバスト統計
統計モデリング
実データ解析
研究分野とその概要
数理統計学を基盤として多変量統計解析、高次元統計、ロバスト統計、ベイズ統計などを研究しています。特に,複雑なデータ構造に対して頑健かつ精度の高い推測手法を開発し、スポーツデータ、 海洋データ、医療データなどの実データ解析に応用することを目指しています。統計モデルの理論的解析と実践的なデータ解析の両面から統計・AI・データサイエンスの発展に貢献することを目標としています。
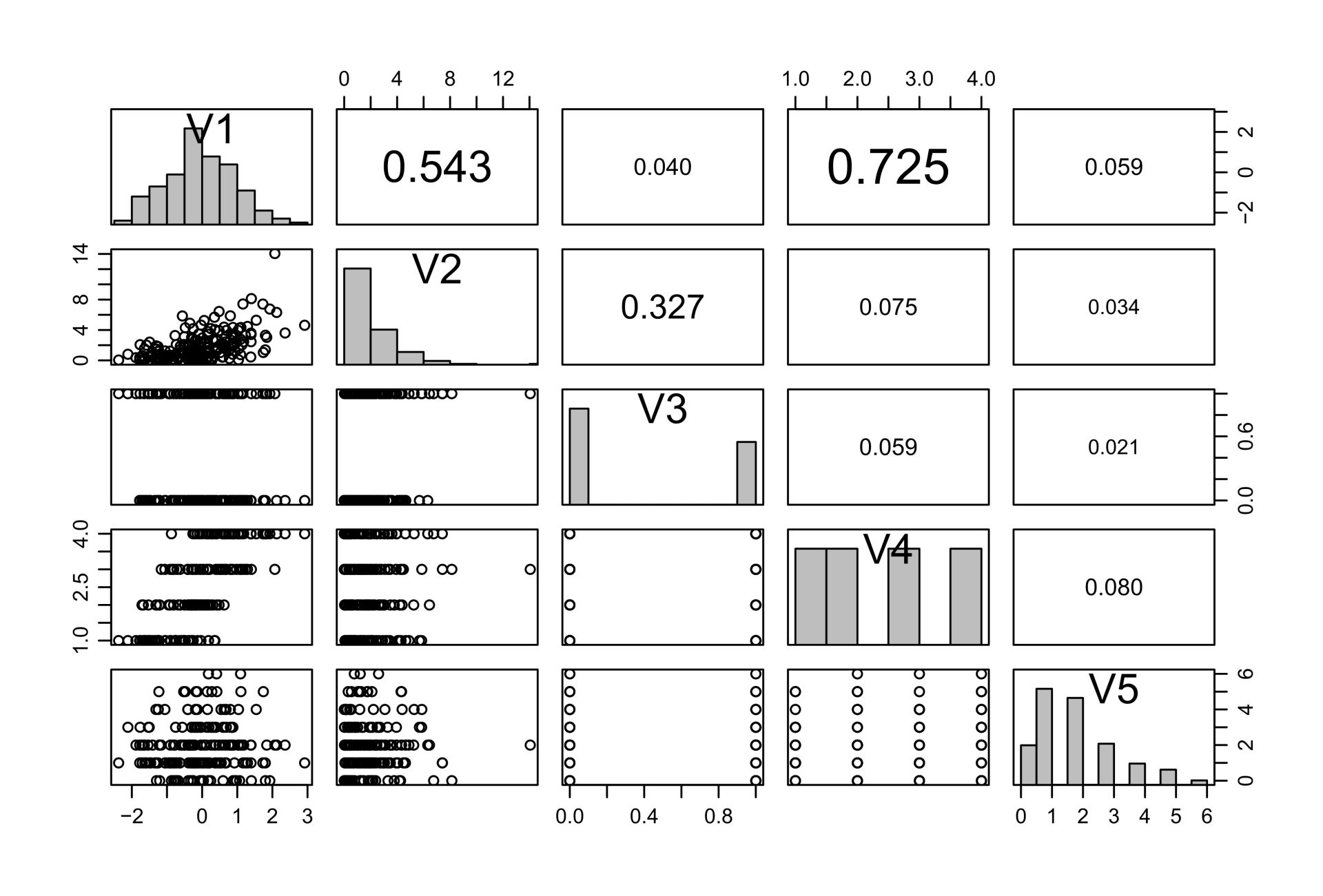
多変量統計解析
多変量統計解析は複数の変数を同時に観察し分析するための統計手法であり、複雑なデータ構造を解明するために非常に有効です。この解析の目的は変数同士の関係やそれぞれの背景を理解し、それらがどのように関連しているかを探ることにあります。一般的に多変量データでは変数間に複雑な相互作用が存在することが多く、その関係を無視すると誤った結論に導かれる可能性があります。したがって多変量統計解析では、変数間の相関や依存性を同時に評価しより正確な解析を行います。複雑なデータ構造を持つ分野、例えば生物学、経済学、工学などにおいて多変量統計解析は重要な役割を果たしており、研究や実務に広く応用されています。
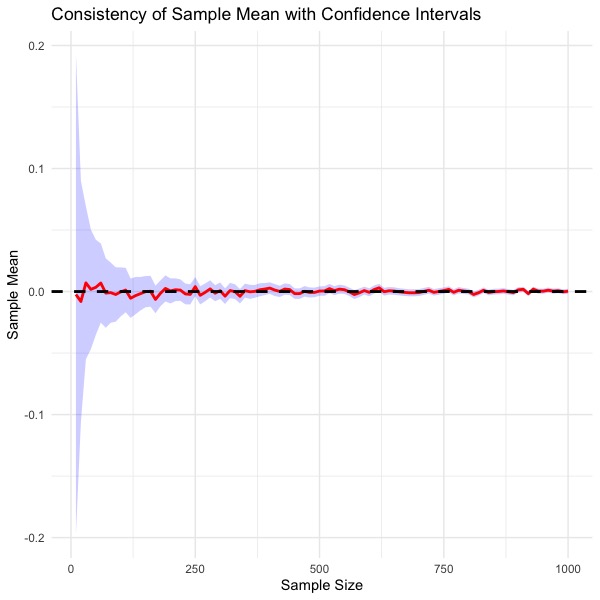
漸近理論解析
複雑なモデルや設定は正確に扱うことが難しく、多くの場合で近似法が用いられています。この際、漸近理論はそのような近似手法に対して理論的な妥当性を提供することを目的としています。従来の漸近理論が適用できない、もしくはそのままでは不十分な新しい問題に対応するために、新たな漸近理論を研究・開発しています
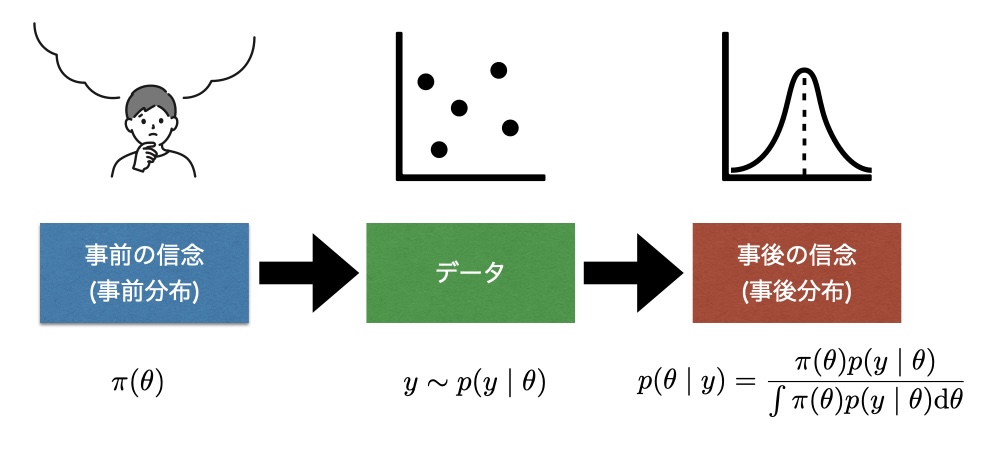
ベイズ統計
ベイズ統計は事前に持っている信念(事前分布)に基づいて、新しい情報やデータが得られた際に、その情報を使って信念を更新し、新しい推定(事後確率)を導く手法です。この推論はベイズの定理を使って行われます。つまり観測されたデータに基づいて事前に想定していた確率を修正し、より正確な推論を行うことが特徴です。近年、計算機技術の進歩により複雑な計算を要するベイズ推定がより手軽に行えるようになり、複雑なモデルやデータに対しても、より精度の高いベイズ推論が適用されています。